№105 Геометрия 7 класс Атанасян
|
Прочитаем задачу №105 для седьмого класса учебника Атанасян:
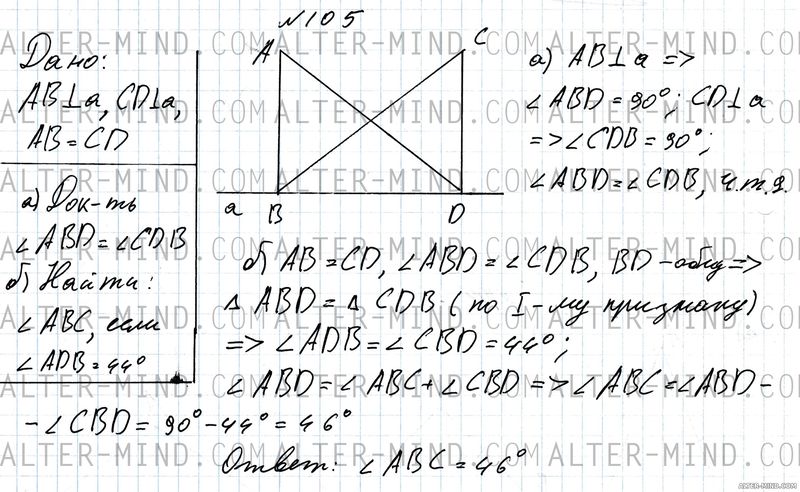
Точки A и C лежат по одну сторону от прямой a. Перпендикуляры AB и CD к прямой a равны. а) Докажите, что ∠ABD = ∠CBD; б) найдите ∠ABC, если ∠ABD = 44°. Объяснение:
Строим прямую a, с одной стороны от прямой отмечаем точки A и C и проводим через них перпендикуляры к прямой а: AB ┴ a, CD ┴ a.
а) так как AB перпендикулярно прямой a ∠ABD = 90°. Аналогично CD ┴ a => ∠CDB = 90°, следовательно углы ABD и CDB равны, что и требовалось доказать. б) отрезки AB и CD равны, углы ABD и CDB равны, BD - общая сторона, следовательно треугольники ABD и CBD равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны, следовательно угол ADB равен углу CDB. Угол ABD состоит из углов ABC и CBD. Зная углы ABD и CBD можем найти ∠ABC = ∠ABD - ∠CBD | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (03.10.2018) | |
| Просмотров: 2702 |
| Всего комментариев: 0 | |