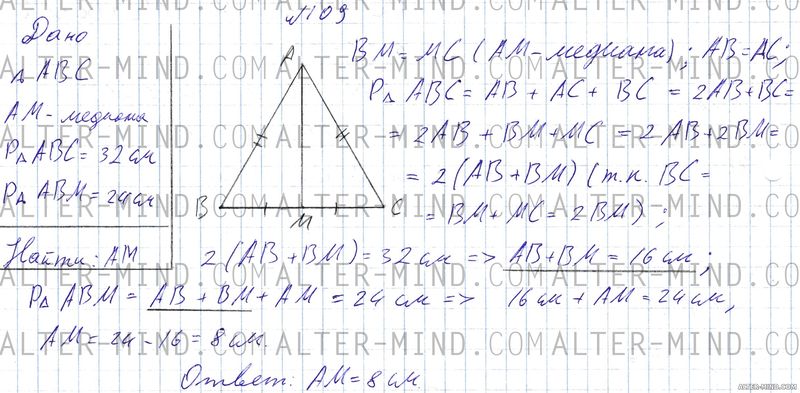№109 Геометрия 7 класс Атанасян
|
Прочитаем задачу №109 для седьмого класса учебника Атанасян:
В равнобедренном треугольнике ABC с основанием BC проведена медиана AM. Найдите медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см. Объяснение:
Строим равнобедренный треугольник ABC и проводим медиану AM. BM = MC (медиана делит сторону пополам), AB = AC. Периметр треугольника ABC = AB + BC + AC = 2AB + BC = 2AB + BM + MC = 2AB + 2BM = 2(AB + BM) (так как BC = BM + MC = 2BM). Зная периметр треугольника ABC можем выразить AB + BM.
Периметр треугольника ABM = AB + BM + AM. Зная сумму AB + BM можем найти AM = PΔABM - (AB + BM). Решение:
 Открыть картинку в новой вкладке Другие номера доступны по ссылке | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (07.10.2018) | |
| Просмотров: 1371 |
| Всего комментариев: 0 | |