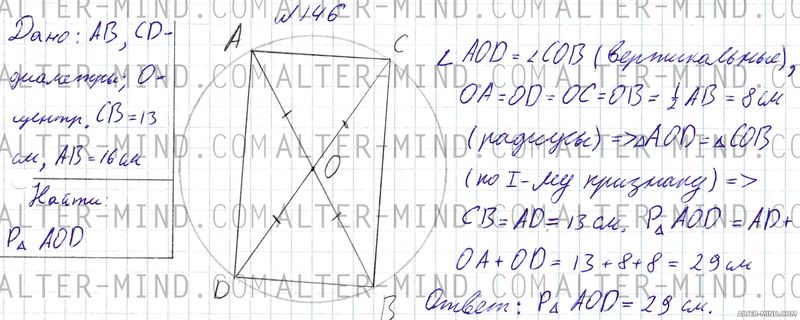
Строим окружность с центром в точке O. Проводим диаметры AB и CD, проводим хорды AC, CB, BD и AD.
Углы AOD и COB равны (вертикальные). OA = OD = OC = OB = 1/2 AB (радиусы), следовательно треугольники AOD и COB равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: CB = AD. Периметр треугольника - сумма длин всех сторон: P_ΔAOD = AD + OA + OD.
Ответ: 29 см.

Решение: 

Открыть картинку в новой вкладке
Другие номера доступны по ссылке