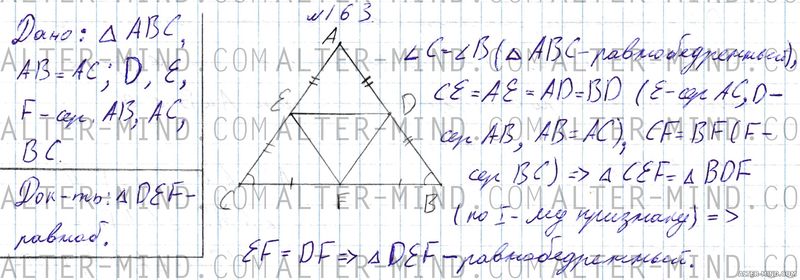
№163 Геометрия 7 класс Атанасян
|
Прочитаем задачу №163 для седьмого класса учебника Атанасян:
Объяснение:
Построим равнобедренный треугольник с основанием BC. Отметим точки D, E и F - середины сторон AB, AC и BC соответственно. Углы С и B равны (свойство равнобедренного треугольника), CE = AE = AD = BD (точки E и D делят равные стороны AC и AB на равные части), CF = BF (F - середина BC), следовательно треугольники CEF и BDF равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: EF = DF, следовательно треугольник DEF равнобедренный по определению, что и требовалось доказать.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (18.11.2018) | |
| Просмотров: 1666 |
| Всего комментариев: 0 | |