Медиана, биссектриса и высота треугольника. Равнобедренный треугольник
|
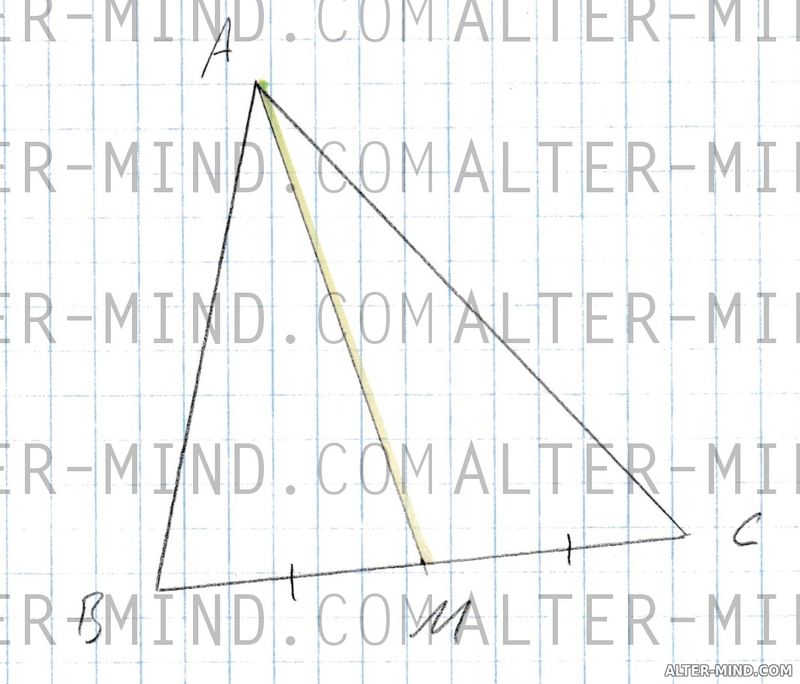
Медиана треугольника это отрезок, соединяющий вершину с серединой противоположной стороны. Иными словами, медиана делит сторону треугольника пополам. Медианы треугольника всегда пересекаются в одной точке.
 Биссектриса делит угол пополам. Биссектрисой треугольника называют отрезок биссектрисы угла соединяющий вершину треугольника с точкой противоположной стороны. Биссектрисы треугольника всегда пересекаются в одной точке. 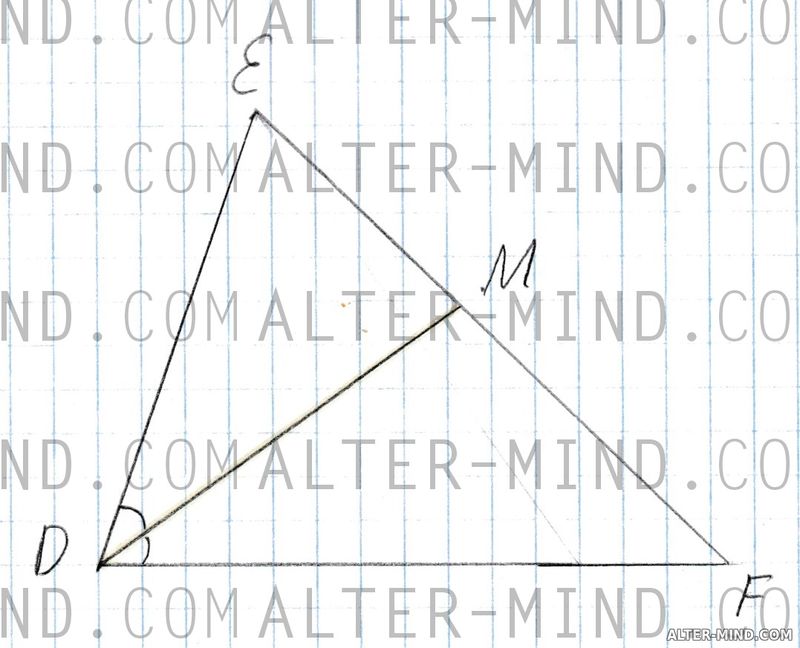
Высота треугольника - перпендикуляр поведенный из вершины треугольника к прямой содержащей противоположную сторону. Иными словами, высота это перпендикуляр проведенный из вершины к противоположной стороне или её продолжению (в тупоугольном треугольнике). Высоты треугольника всегда пересекаются в одной точке. 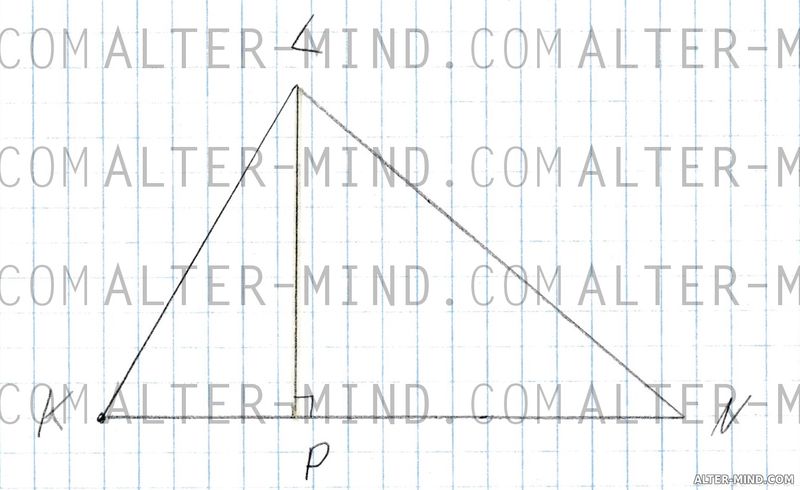
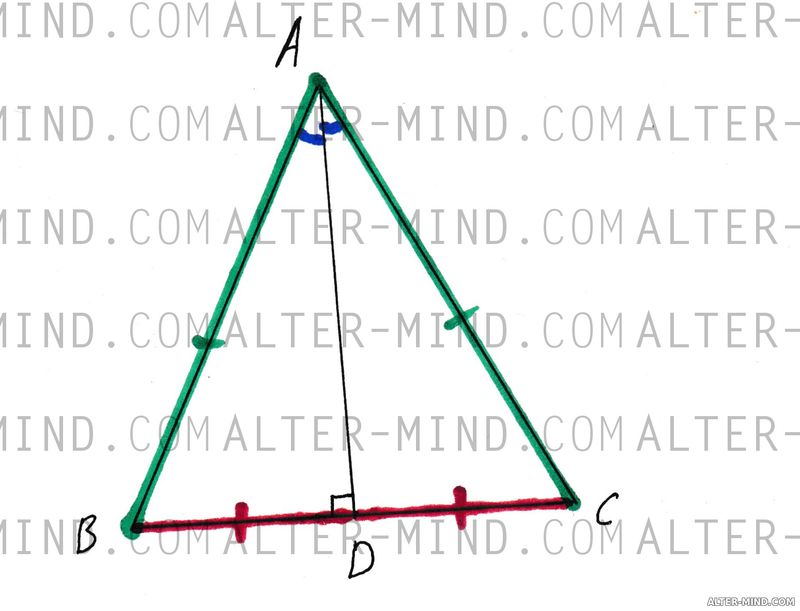
Равнобедренный треугольник - такой треугольник у которого две стороны равны. Равные стороны принято называть боковыми сторонами, третью сторону - основанием. Свойства равнобедренного треугольника:
Равные элементы выделены одним цветом.
 Равносторонний треугольник - частный случай равнобедренного треугольника. В равностороннем треугольнике все стороны и углы равны. Медианы, биссектрисы и высоты, проведенные к каждой стороне (каждую сторону можно считать основанием, так как две другие равны) совпадают (выделены цветом), все они равны между собой и пересекаются в одной точке. 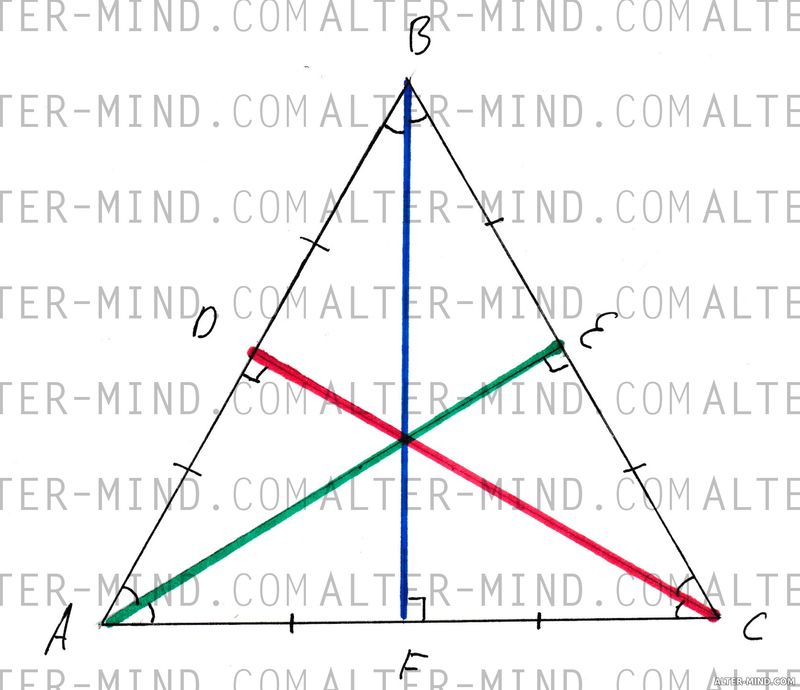
Теория - оглавление Список разобранных задач | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (16.10.2018) | |
| Просмотров: 9727 |
| Всего комментариев: 0 | |