Прочитаем задачу №96 для седьмого класса учебника Атанасян:

Объяснение:

---

---

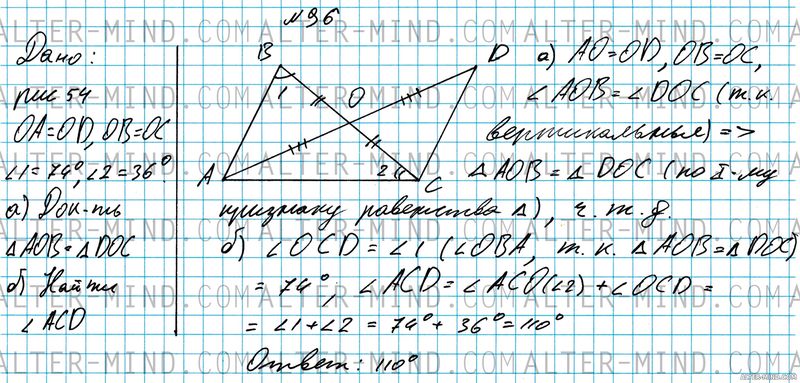
Рассмотрим рисунок 54: а) OA = OD, OB = OC, углы AOB и DOC равны (вертикальные), следовательно равны и треугольники AOB и DOC (по первому признаку равенства треугольников), что и требовалось доказать.
б)В равных треугольниках (см. букву а) ) соответствующие элементы равны ∠OCD = ∠1 (∠1 и ∠OBA - это один и тот же угол, аналогично ∠2 и ∠ACO один и тот же угол). По рисунку 54 (чертежу в решении) видно, что ∠ACD = ∠ACO + ∠OCD = ∠1 + ∠2.

Решение:

Открыть картинку в новой вкладке
Другие номера доступны по ссылке