Урок 3. Плоскость. Прямая. Луч
План урока:
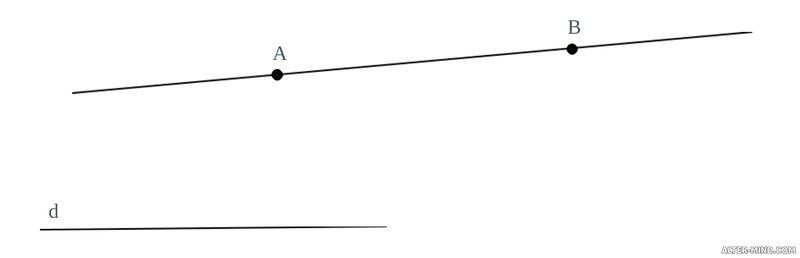
ПрямаяЧерез две точки можно провести по линейке прямую линию. Прямая, в отличие от отрезка, не имеет длины и неограниченно продолжается в обе стороны. Прямую обычно обозначают двумя заглавными буквами латинского алфавита, которые обозначают названия точек, лежащих на этой прямой. Допустимо обозначать прямую одной строчной латинской буквой. Так, на рисунке ниже изображены две прямые: AB и d.
 Если две прямые имеют общую точку, то говорят, что они пересекаются в этой точке. 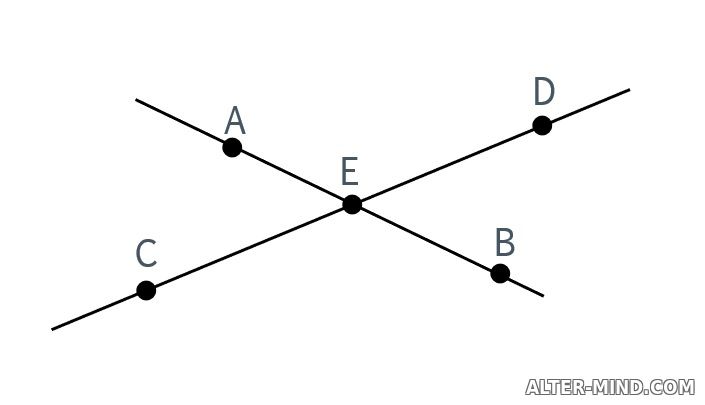 Записывают это так: AB ∩ CD = E, где ∩ математический символ, обозначающий пересечение. Через две различные точки можно провести только одну прямую ПлоскостьПлоскость - это любая прямая поверхность. Так, поверхность стола, стена, оконное стекло - всё это даёт нам представление о плоскости.
Вообще плоскость - это поверхность, содержащая полностью каждую прямую, соединяющую любые её (плоскости) точки. Это определение может показаться довольно сложным, но из него становится понятно, что математическая плоскость, в отличие от плоскости стола, безгранично простирается в любом направлении. ЛучТочка делит прямую на два луча.
 Саму точку называют началом луча. В отличие от прямых и отрезков порядок букв в обозначении луча имеет значение. Первой записывают точку, обозначающую начало луча, второй - любую точку, лежащую на этом луче. На рисунке выше точка O делит прямую на лучи OA и OB. Лучи, на которые точка разбивает прямую называют дополнительными. Так, OA и OB - дополнительные лучи. На рисунке ниже изображён луч CM.  Луч имеет начало, но не имеет конца. Лучше всего это явление демонстрирует лазерная указка. Лазерный луч "начинается" в корпусе фонарики и, если не встречает препятствий на пути, уходит в бесконечность.  Примеры решения заданийЗадание 1
Отметьте в тетради точки A и B. Проведите прямую AB. Отметьте на отрезке AB точку С. Лежит ли точка C на отрезке AB? Возможно ли отметить на прямой AB точку D так, чтобы она не лежала на отрезке AB? Построим прямую AB, выделим отрезок цветом. Отметим точку C на отрезке и точку D на прямой. 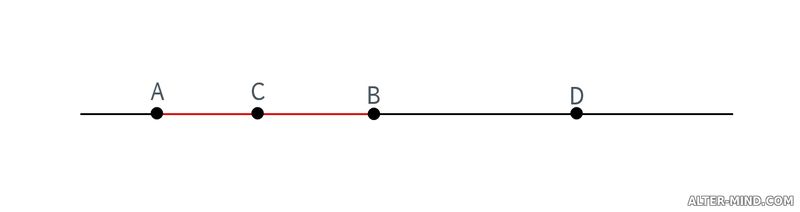 Задание 2 Какие из точек, изображенных на рисунке лежат на прямой AB, а какие нет? 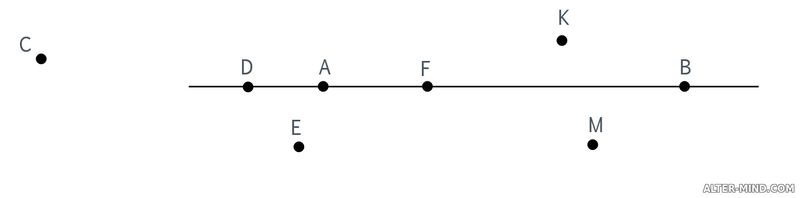 A, B, D, F ∈ AB, C, E, K, M ∉ AB, где "∈" - математический символ, означающий "принадлежит", а "∉" математический символ, обозначающий не принадлежит. Задание 3 На сколько частей делят плоскость две пересекающиеся прямые? 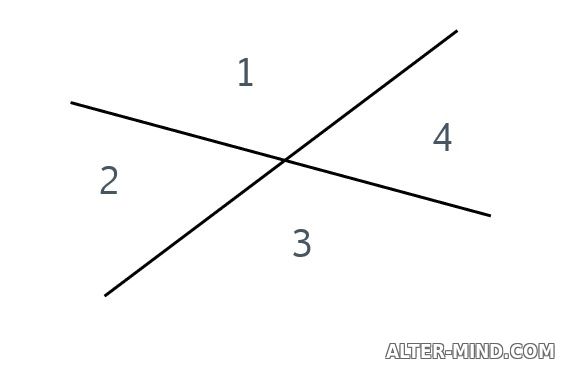 Ответ: на 4 части
Задание 4 Из города А в город В выехали автомобилист со скоростью 80 км/ч и мотоциклист со скоростью 60 км/ч. Сколько времени затратил на путь мотоциклист, если автомобилист приехал через 6 часов после старта? 1) 80 * 60 = 480 (км) - расстояние между городами A и B 2) 480 : 6 = 8 (ч) - время мотоциклиста Ответ: 8 часов.
Задание 5 Начертите пятиугольник ABCDE. Отметьте точку M на стороне AB и точку N на стороне CD. Соедините M и N отрезком. Какие получились многоугольники? Назовите их. Построим пятиугольник, отметим точки M и N и проведём отрезок MN: 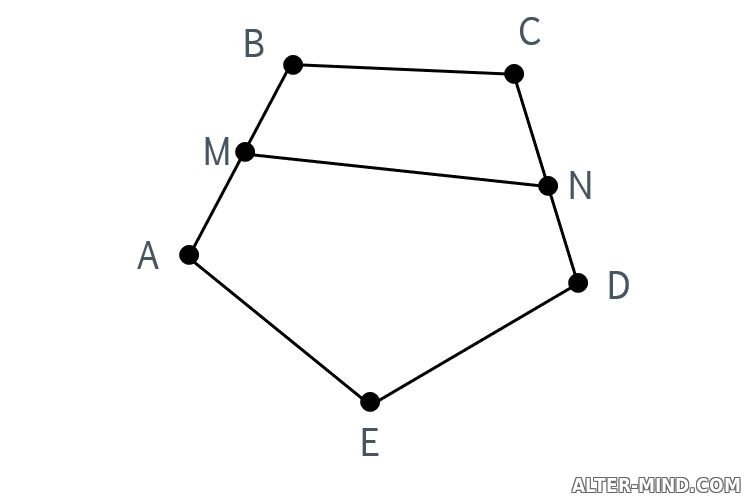 Ответ: четырёхугольник MBCN, пятиугольник AMNDE
Задание 6
Начертите прямую и отметьте на ней точки A, B, C и D. Сколько различных обозначений прямой можно составить? Запишите любые 3. Построим прямую и отметим точки:  Прямую обозначают двумя буквами - точками, лежащими на этой прямой. Так, на первое место можем выбрать любую из четырёх букв, на второе - любую из трех оставшихся. Получаем: 1) 4 * 3 = 12 - различных обозначений можно составить. Запишем некоторые из них: AD, BC, DB. Задание 7 Начертите луч AB. Отложите на нём последовательно 2 отрезка по 3 см. Сколько таких отрезков можно отложить на этом луче? Начертим луч, отметим 2 отрезка:  Луч имеет начало, но не имеет конца, следовательно можно отложить бесконечно много таких отрезков. Задание 8 Может ли сумма двух чисел равняться разности этих же чисел? Произведению этих чисел? Приведите примеры таких чисел. Сумма двух чисел может равняться разности двух чисел только в том случае, когда второе слагаемое (вычитаемое) равно нулю. 1) 3 + 0 = 3 - 0 = 3 В натуральных числах можно подобрать единственное решение: 2) 2 + 2 = 2 * 2 = 4, но если использовать дроби, можно найти бесконечно много таких решений. Домашнее заданиеИз учебника: 78, 79, 81, 85, 88, 92, 97, 104, 105
№1 Постройте четырёхугольник. Через каждые две точки проведите прямые. На сколько частей эти прямые делят плоскость? №2 Отметьте три точки не лежащие на одной прямой. Через каждые две точки проведите прямые. Назовите все получившиеся лучи. Приведите 3 примера дополнительных лучей. №3 В три банки с надписями "малиновое", "клубничное" и "малиновое или клубничное" налили смородиновое, малиновое и клубничное варенье. Все надписи оказались неправильными. Какое варенье налили в банку "клубничное"? Видеоурок | |
| Категория: Математика 5 класс | Добавил: altermind (06.05.2020) | |
| Просмотров: 1958 | |
| Всего комментариев: 0 | |