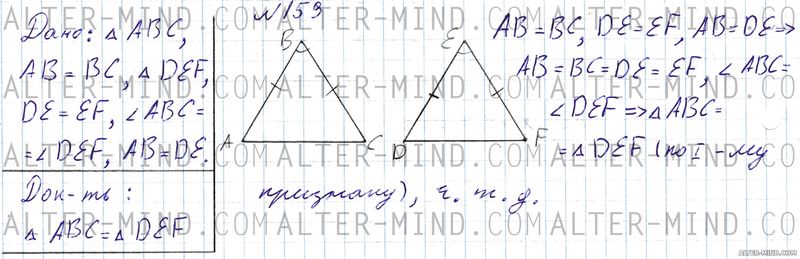
№159 Геометрия 7 класс Атанасян
|
Прочитаем задачу №159 для седьмого класса учебника Атанасян:
Объяснение:
Построим два равных (их равенство и будет доказывать) равнобедренных треугольника ABC и DEF так, что: AB = BC, DE = EF, ∠ABC = ∠DEF и AB = DE.
Получаем, что все боковые стороны обоих треугольников равны между собой. Кроме того равны и ∠ABC = ∠DEF, следовательно треугольники ABC и DEF равны по первому признаку равенства треугольников, что и требовалось доказать. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (15.11.2018) | |
| Просмотров: 1181 |
| Всего комментариев: 0 | |