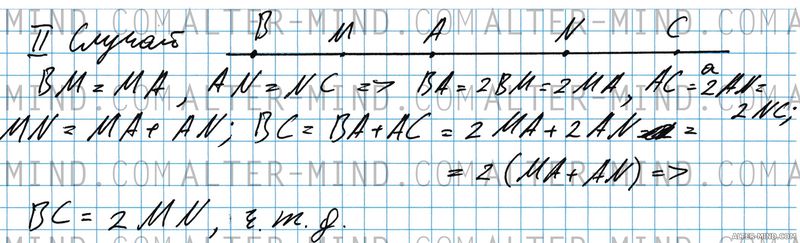№79 Геометрия 7 класс Атанасян
|
Прочитаем задачу №79 для седьмого класса учебника Атанасян:
Объяснение:
В первом случае, представленном в решении BC не будет равняться 2MN (Хотя в некоторых решебниках и ГДЗ будет доказан этот случай. Такое доказательство неверно.)
Во втором случае точка A принадлежит отрезку BC. Поскольку точки M и N середины отрезков AB и AC будут справедливыми следующие равенства: AN = NC и BM = MA. Следовательно, BA = 2BM = 2MA, AC = 2AN = 2NC. MN = MA + AN. Получаем, что BC = BA + AC = 2MA + 2AN = 2(MA + AN) = 2MN, что и требовалось доказать. Возможно построить ещё и третий случай, который нам не подойдет, как и первый. (подумайте какой и почему не подойдет). В тетрадь можно переписать только второй случай, не упоминая об остальных. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (25.09.2018) | |
| Просмотров: 1636 |
| Всего комментариев: 0 | |