№98 Геометрия 7 класс Атанасян
|
Прочитаем задачу №98 для седьмого класса учебника Атанасян:
Объяснение:
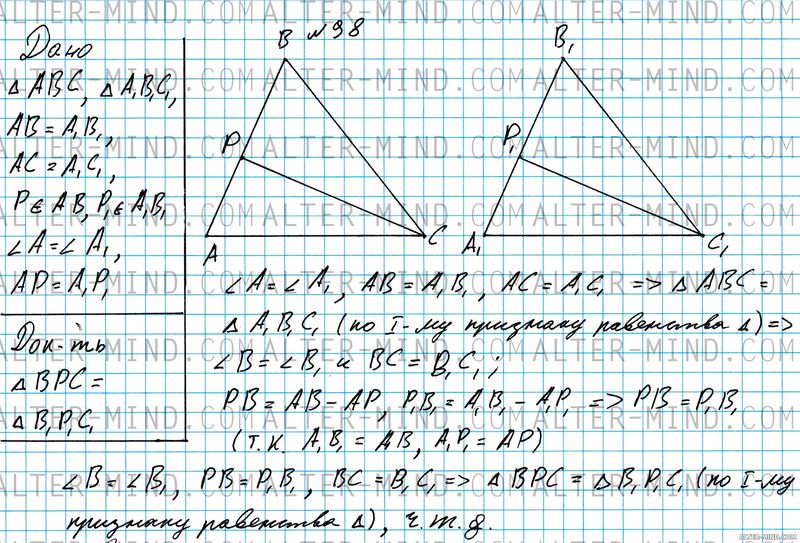
Строим два одинаковых треугольника: ABC и A1B1C1, на сторонах AB и A1B1 отмечаем точки P и P1 на одинаковом расстоянии от точек A и A1. Проще говоря, у нас должно получиться два одинаковых чертежа, один обозначен обычными буквами, другой "клон", обозначен этими же буквами с индексом 1.
Рассмотрим получившиеся треугольники: ∠A = ∠A1, AB = A1B1 и AC = A1C1, следовательно треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны, следовательно ∠B = ∠B1 и BC = B1C1. По построению видно: PB = AB - AP, аналогично P1B1 = A1B1 - A1P1, следовательно PB = P1B1, (так, как AB = A1B1, AP = A1P1). ∠B = ∠B1, PB = P1B1 и BC = B1C1 следовательно ΔBPC = ΔB1P1C1 по первому признаку равенства треугольников. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (01.10.2018) | |
| Просмотров: 1536 |
| Всего комментариев: 0 | |