№139 Геометрия 7 класс Атанасян
|
Прочитаем задачу №139 для седьмого класса учебника Атанасян:
Объяснение:
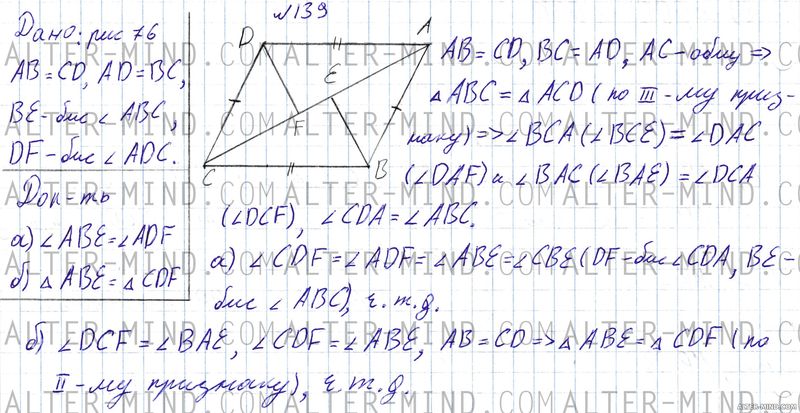
Рассмотрим рисунок 76 (см. чертеж в решении). AB = CD, BC = AD, AC - общая сторона, следовательно треугольники ABC и ACD равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны, следовательно ∠BCA (он же является углом BCE, см. чертеж. Далее в скобках указаны другие варианты записи углов) = ∠DAC (∠DAF) и ∠BAC (∠BAE) = ∠DCA (∠DCF), ∠CDA = ∠ABC.
а) ∠CDF = ∠ADF = ∠ABE = ∠CBE (DF и BE биссектрисы равных углов СDA и ABC делят их на равные части), что и требовалось доказать. б)Углы DCF и BAE равны, углы CDF и ABE равны, AB = CD, следовательно треугольники ABE и CDF равны по второму признаку равенства треугольников, что и требовалось доказать. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (28.10.2018) | |
| Просмотров: 4080 |
| Всего комментариев: 0 | |