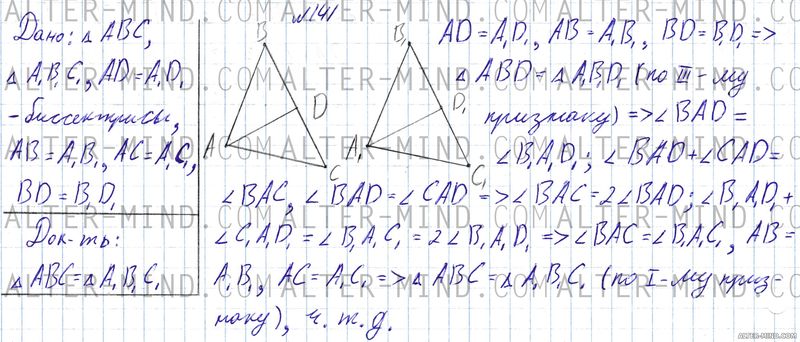Прочитаем задачу №141 для седьмого класса учебника Атанасян:

Объяснение:

---

---

 

Строим равные треугольники ABC и ABC (будем доказывать их равенство) и проводим равные биссектрисы AD и AD.
AD = AD, AB = AB, BD = BD, следовательно треугольники ABD и ABD равны по третьему признаку равенства треугольников. В равных треугольников соответствующие элементы равны, следовательно углы BAD и BAD равны. Угол BAC состоит из равных углов BAD и CAD (AD - биссектриса), аналогично угол BAC состоит из равных углов BAD и CAD (AD - биссектриса), следовательно углы BAC и BAC равны, AB = AB, AC = AC, следовательно треугольники ABC и ABC равны по первому признаку равенства треугольников, что и требовалось доказать.

Решение:

Открыть картинку в новой вкладке
Другие номера доступны по ссылке