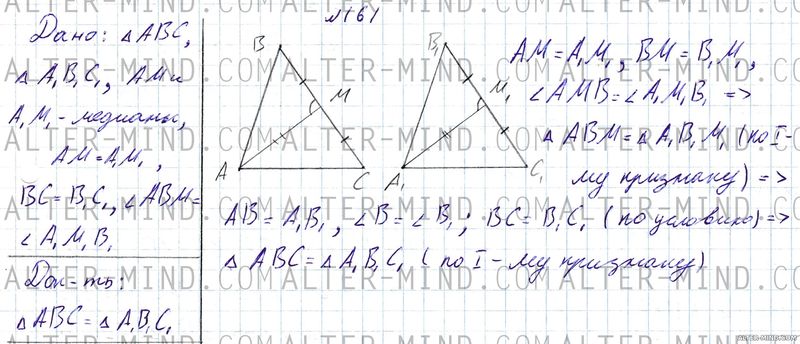
№161 Геометрия 7 класс Атанасян
|
Прочитаем задачу №162 для седьмого класса учебника Атанасян:
Объяснение:
AM = AM, BM = BM, ∠AMB = ∠A1M1B1, следовательно треугольники ABM и ABM равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: AB = AB, ∠B = ∠B1; BC = BC (по условию), следовательно треугольники ABC и ABC равны по первому признаку равенства треугольников.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (18.11.2018) | |
| Просмотров: 1327 |
| Всего комментариев: 0 | |