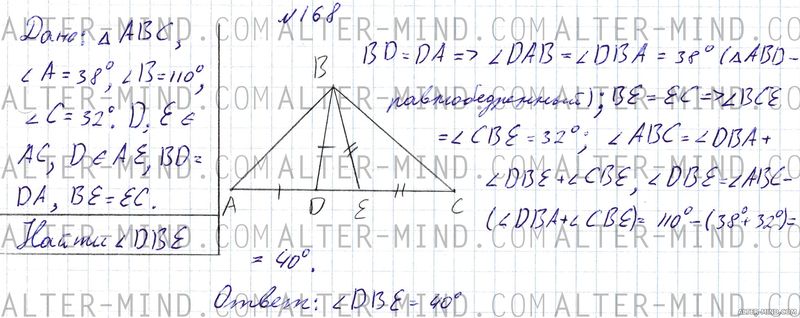
№168 Геометрия 7 класс Атанасян
|
Прочитаем задачу №168 для седьмого класса учебника Атанасян:
Объяснение:
Строим треугольник, как сказано в условии (приблизительное построение есть в решении). Треугольник ABD равнобедренный (BD = DA по условию) следовательно углы DAB и DBA равны. Треугольник BCE тоже равнобедренный (BE =EC) следовательно углы BCE и CBE равны. Угол ABC состоит из углов DBA, DBE и CBE. Получаем что ∠DBE = ∠ABC - (∠DBA + ∠CBE).
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (21.11.2018) | |
| Просмотров: 1959 |
| Всего комментариев: 0 | |