|
Прочитаем задачу №185 для седьмого класса учебника Атанасян:
С помощью циркуля и линейки разделите данный отрезок на четыре равные части.
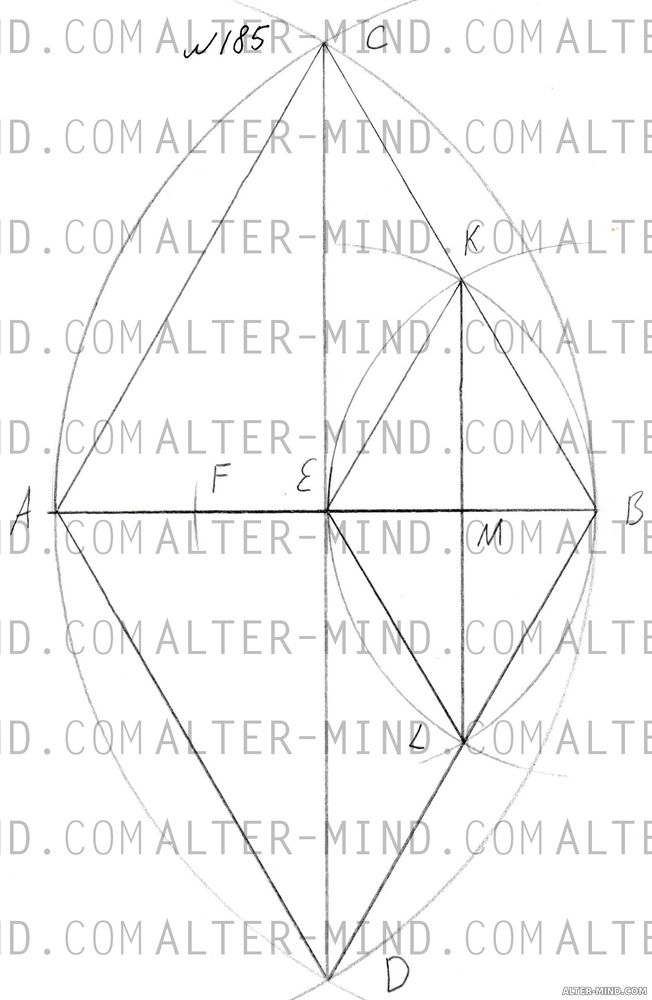
- Примем AB за радиус. Проведём пересекающиеся дуги окружностей радиуса AB с центрами в точках A и B. Точки пересечения дуг обозначим C и D. Проведём AC, BC, AD, BD и CD. Отрезки CD и AB пересекаются, точку пересечения обозначим E.
- Примем BE за радиус. Проведём пересекающиеся дуги окружностей радиуса BE с центрами в точках B и E. Точки пересечения обозначим K и L. Проведём EK, BK, EL, BL и KL. Отрезки KL и BE пересекаются, точку пересечения обозначим M. Проведём дугу окружности радиуса BE с центром в точке M так, чтобы она пересекала отрезок AM, точку пересечения обозначим F.
- Докажем, что отрезки AF, FE, EM и MB - искомые: AC = BC = AD = BD (= AB, радиусы), CD - общая сторона, следовательно треугольники ACD и BCD равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠ACD (совпадает с углом ACE) = ∠BCD (совпадает с углом BCE), следовательно CE - медиана, биссектриса и высота равнобедренного треугольника ABC (AC = BC), следовательно AE = BE. EK = BK = EL = BL (= BE, радиусы), KL - общая сторона, следовательно треугольники EKL и BKL равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠EKL (совпадает с углом EKM) = ∠BKL (совпадает с углом BKM), следовательно KM - медиана, биссектриса и высота равнобедренного треугольника BEK (EK = BK), следовательно EM = MB. FM = BE = AE (радиусы). FM = FE + EM, BE = EM + MB, следовательно FE = MB = EM. AE = AF + FE, FM = FE + EM, следовательно AF = EM. Откуда получаем: AF = FE = EM = MB, AB = AF+FE+EM+MB. То есть данный отрезок AB разделен точками F, E и M на 4 равных отрезка, что и требовалось доказать.
|