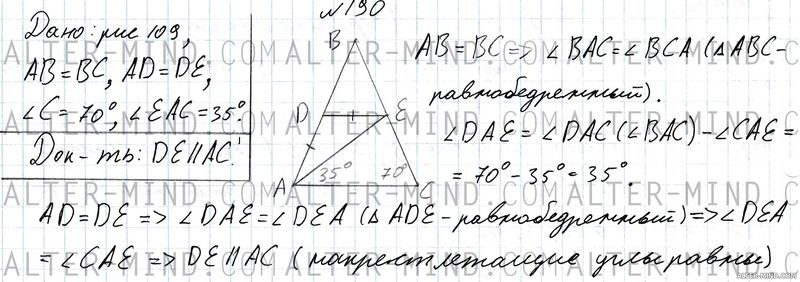Прочитаем задачу №190 для седьмого класса учебника Атанасян:

Объяснение:

---

---

Рассмотрим рисунок 109 учебника (см. чертеж в решении): AB = BC, следовательно углы BAC и BCA при основании равнобедренного треугольника ABC равны. ∠DAE = ∠DAC (совпадает с углом BAC) - ∠CAE = 35°. AD = DE, следовательно углы DAE и DEA при основании равнобедренного треугольника ADE равны. Получаем, что накрест лежащие углы DEA и CAE равны, следовательно отрезки DE и AC параллельны.

Решение: 

Открыть картинку в новой вкладке
Другие номера доступны по ссылке