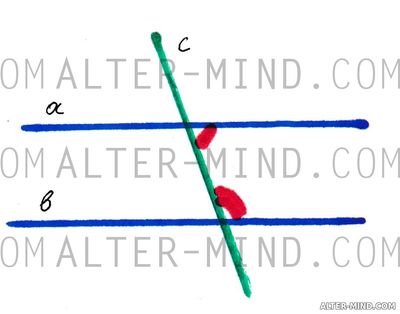
Углы при пересечении двух прямых секущей

• Накрест лежащие углы: 3 и 5, 4 и 6;
• Внутренние односторонние углы: 3 и 6, 3 и 5;
• Соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8.
• Внешние односторонние углы: 1 и 8, 2 и 7.

Примечание: в учебнике Атанасяна дано понятие только внутренних односторонних углов, там они называются просто односторонними. Тем не менее, все описанные утверждения и теоремы справедливы и для внешних односторонних углов, что легко доказывается через смежные углы.

Признаки параллельности прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей.

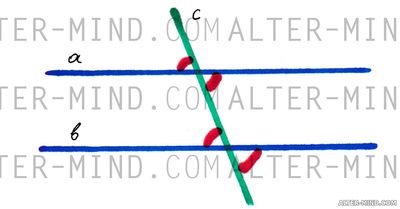
Теорема:

• Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

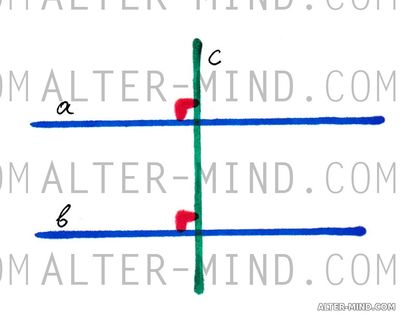
Следствие:

• Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.

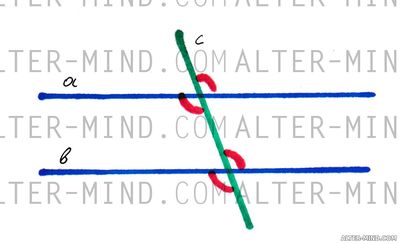
Теорема:

• Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то соответственные углы равны.

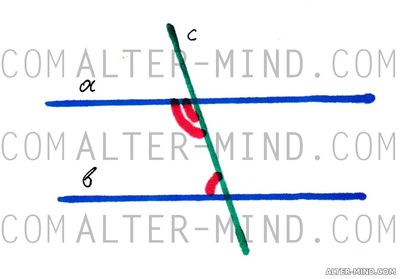
Теорема:

• Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Аксиомы

• Через любые две точки проходит прямая, и при том только одна.
• На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
• От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

Аксиома о параллельных прямых:

• Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну. (эта аксиома вытекает из знаменитого 5-го постулата Евклида).

1. Если прямая пересекают одну из двух параллельных прямых, то она пересекает и другую.
2. Если две прямые параллельны третьей, то они параллельны.