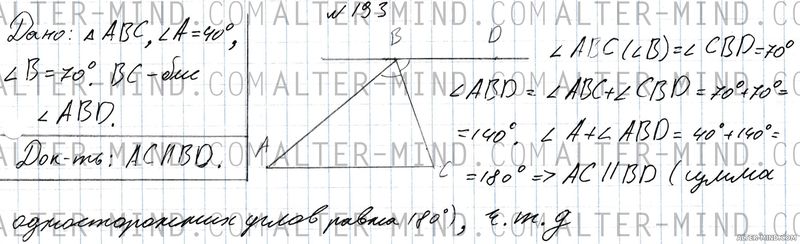
№193 Геометрия 7 класс Атанасян (Разбор и объяснение)

№193 Геометрия 7 класс Атанасян

Прочитаем задачу №193 для седьмого класса учебника Атанасян: В треугольнике ABC ∠A = 40°, ∠B = 70°. Через вершину B проведена прямая BD так, что луч BC - биссектриса угла ABD. Докажите, что AC \|\| BD. Объяснение: ∠ABC (∠B) = ∠CBD = 70°. ∠ABD = ∠ABC + ∠CBD = 70° + 70° = 140° (BC - биссектриса угла ABD). ∠A + ∠ABD = 40° + 140° = 180°, следовательно AC и BD параллельны (так как сумма односторонних углов равна 180°), что и требовалось доказать. Объяснение: Открыть картинку в новой вкладке Другие номера доступны по ссылке
Категория: Геометрия 7-9 Атанасян \| Добавил: altermind (14.12.2018)
Просмотров: 1645