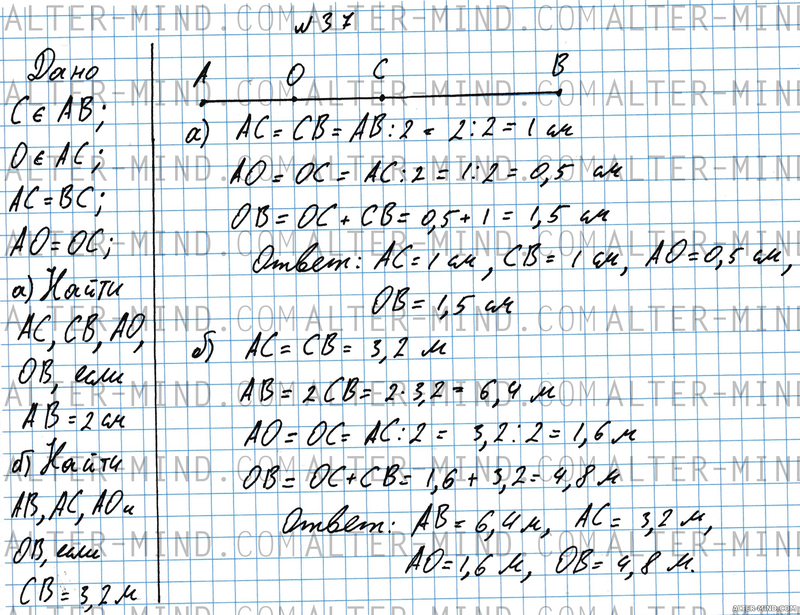№37 Геометрия 7 класс Атанасян
|
Прочитаем задачу №37 для седьмого класса учебника Атанасян:
Точка C - середина отрезка AB, точка O - середина отрезка AC. а) Найдите AC, CB, AO и OB, если AB = 2 см; б) Найдите AB, AC, AO и OB, если CB = 3.2 м Объяснение:
Построим отрезок AB (схематично, удобно взять 8 см). Посередине отмечаем точку C (на расстоянии 4 см от точки A). Посередине отрезка AC отмечаем точку O (на расстоянии 2 см от точки A).
а) AC = BC = AB:2 = 2:2 = 1 см (по условию точка C середина отрезка AB). AO = OC = AC:2 = 0.5 см (по условию точка O середина отрезка AC). По чертежу видно, что отрезок OB состоит из двух отрезков: OC и BC. OB = OC + BC = 0.5 + 1 = 1.5 см. б) AB = 2BC = 2*3.2 = 6.4 м (по условию точка C середина отрезка AB, а значит AC = BC). AO = OC = 3.2:2 = 1.6 м (по условию точка O середина отрезка AC). Аналогично предыдущему пункту находим OB = OC + BC = 1.6+3.2 = 4.8 м. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (11.09.2018) | |
| Просмотров: 1633 |
| Всего комментариев: 0 | |