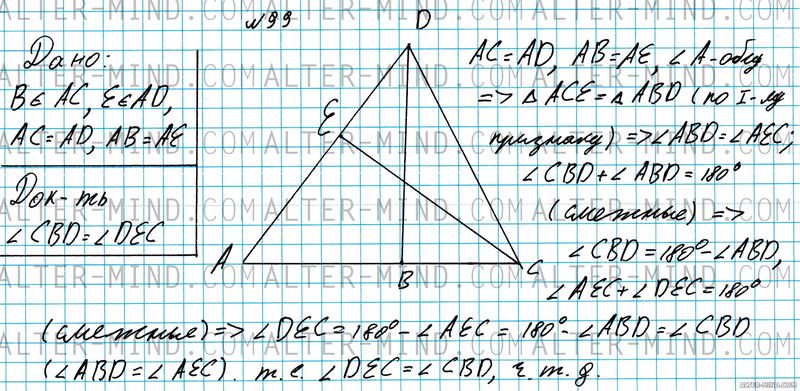Объяснение:

---

---

Строим угол DAC (AC = AD), на противоположных сторонах угла, на равном расстоянии от точки А отмечаем точки E и B. Через полученные точки проводим отрезки EC, BD, CD. Рассмотрим треугольники ACE и ABD: AC = AD, AB = AE, ∠A - общий, следовательно  ΔACE =  ΔABD по первому признаку равенства треугольников, следовательно углы ABD и AEC равны (в равных треугольниках соответствующие элементы равны).
∠CBD + ∠ABD = 180° (смежные), выражаем ∠CBD = 180° - ∠ABD. Аналогично ∠AEC + ∠DEC = 180° (смежные), => ∠DEC = 180° - ∠AEC = 180° - ∠ABD = ∠CBD, что и требовалось доказать.

Решение:

Открыть картинку в новой вкладке
Другие номера доступны по ссылке