Прочитаем задачу №112 для седьмого класса учебника Атанасян:

Объяснение:

---

---

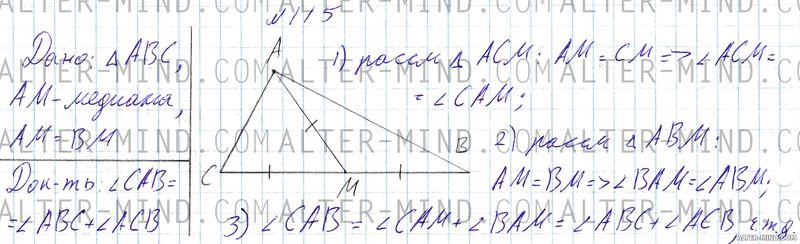
Удобнее всего построение треугольника начинать со стороны BC: строим отрезок BC, в середине отрезка отмечаем точку M. Из точки M откладываем отрезок AM = BM = CM (CM = BM, потому, что медиана делит сторону пополам), так, чтобы точка A не лежала на стороне BC. Проводим отрезки AB и AC.
Рассмотрим треугольник ACM: AM = CM, значит он равнобедренный, а в равнобедренном треугольнике углы при основании равны: ∠ACM = ∠CAM.
Аналогично в треугольнике ABM: AM = BM => ∠BAM = ∠ABM. 
По чертежу ∠CAB = ∠CAM + ∠BAM = ∠ABC + ∠ACB (так как угол ACB и ACM - один и тот же угол, аналогично угол ABC и угол ABM), что и требовалось доказать.

Решение

Открыть картинку в новой вкладке
Другие номера доступны по ссылке