№121 Геометрия 7 класс Атанасян
|
Прочитаем задачу №121 для седьмого класса учебника Атанасян:
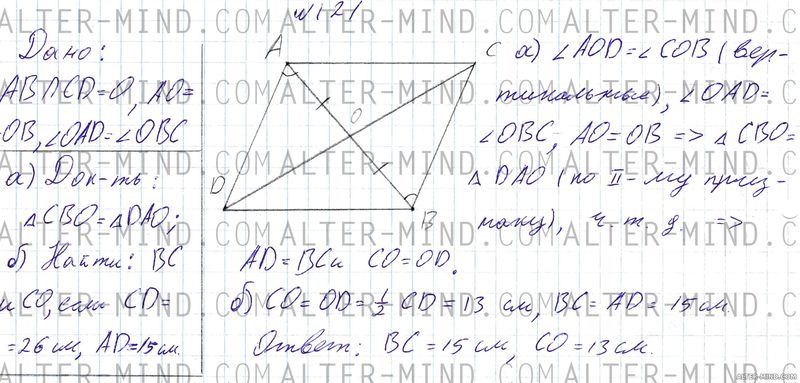
Отрезки AB и CD пересекаются в середине O отрезка AB, ∠OAD = ∠OBC. а) Докажите, что ΔCBO = ΔDAO; б) Найдите BC и CO, если CD = 26 см, AD = 15 см. Объяснение:
Строим отрезок AB, в середине отмечаем точку O. Через эту точку проводим отрезок CD так, чтобы точка O была и его серединой (но не отмечаем этот факт на чертеже, он будет доказан в ходе решения). Проводим отрезки AD, AC, BC и BD.
а) Углы AOD и COB равны (вертикальные), ∠OAD = ∠OBC, AO = OB, следовательно треугольники CBO и DAO равны по второму признаку равенства треугольников, что и требовалось доказать. б) В равных треугольниках соответствующие элементы равны, следовательно AB = CD, AD = BC | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (16.10.2018) | |
| Просмотров: 4220 |
| Всего комментариев: 0 | |