№123 Геометрия 7 класс Атанасян
|
Прочитаем задачу №123 для седьмого класса учебника Атанасян:
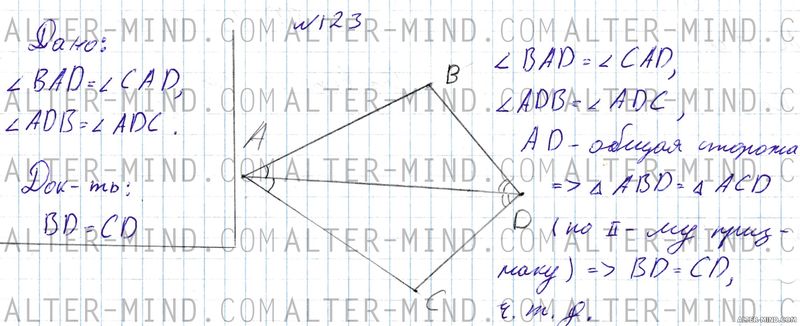
На биссектрисе угла A взята точка D, а на сторонах этого угла - точки B и C такие, что ∠ADB = ∠ADC. Докажите, что BD = CD. Объяснение:
Строим угол A и проводим биссектрису, на которой отмечаем точку D. На сторонах угла отмечаем точки B и C так, что ∠ADB = ∠ADC (это проще построить так чтобы AB = AC, так как треугольники окажутся равными, см чертеж в решении). Углы BAD и CAD равны (AD - биссектриса), углы ADB и ADC равны по условию, AD - общая сторона, следовательно треугольники ABD и ACD равны по второму признаку равенства треугольников. В равных треугольниках соответствующие элементы равны, следовательно BD = СВ.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (17.10.2018) | |
| Просмотров: 2740 |
| Всего комментариев: 0 | |