№130 Геометрия 7 класс Атанасян
|
Прочитаем задачу №130 для седьмого класса учебника Атанасян:
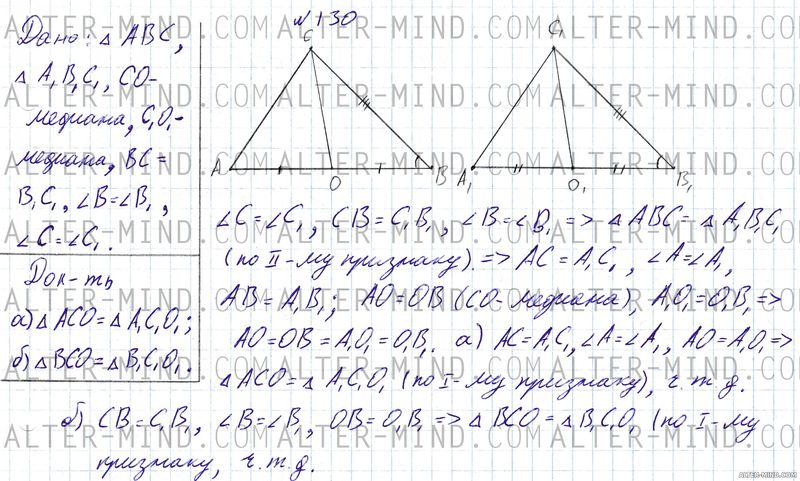
В треугольниках ABC и A1B1C1 отрезки CO и C1O1 - медианы, BC = B1C1, ∠B = ∠B1 и ∠C = ∠C1. Докажите, что: а) ΔACO = Δ A1C1O1; б) ΔBCO = ΔB1C1O1. Объяснение:
Строим два равных треугольника ABC и A1B1C1 и проводим в них медианы CO и C1O1 соответственно (см. чертеж в решении). BC = B1C1, ∠B = ∠B1 и ∠C = ∠C1, следовательно треугольники ABC и A1B1C1 равны по второму признаку равенства треугольников. В равных треугольниках соответствующие элементы равны, следовательно AC = A1C1, углы A и A1 равны, AB = A1B1. AO = OB (CO - медиана), аналогично A1O1 = O1B1, следовательно AO = OB = A1O1 = O1B1.
а) AC = A1C1, углы A и A1 равны, AO = A1O1, следовательно треугольники ACO и A1C1O1 равны по первому признаку равенства треугольников, что и требовалось доказать. б) CB = C1B1, углы B и B1 равны, OB = O1B1, следовательно треугольники BCO и B1C1O1 равны по первому признаку равенства треугольников, что и требовалось доказать. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (22.10.2018) | |
| Просмотров: 1768 |
| Всего комментариев: 0 | |