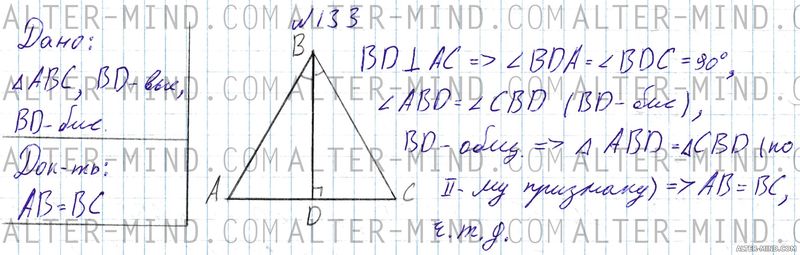№133 Геометрия 7 класс Атанасян
|
Прочитаем задачу №133 для седьмого класса учебника Атанасян:
Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник - равнобедренный. Объяснение:
Эта задача практически полностью аналогична предыдущей. Строим равнобедренный треугольник ABC (ниже докажем, что он равнобедренный) c основанием AC и проводим BD (является биссектрисой и высотой одновременно). Высота перпендикулярна основанию, следовательно углы BDA и BDC равны по 90° каждый. Углы ABD и CBD равны (BD - биссектриса), BD - общая сторона, следовательно треугольники ABD и CBD равны по второму признаку равенства треугольников. В равных треугольниках соответственные элементы равны, следовательно AB = BC, следовательно треугольник ABC равнобедренный по определению, что и требовалось доказать.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (23.10.2018) | |
| Просмотров: 1515 |
| Всего комментариев: 0 | |