Прочитаем задачу №134 для седьмого класса учебника Атанасян:

Объяснение:

---

---

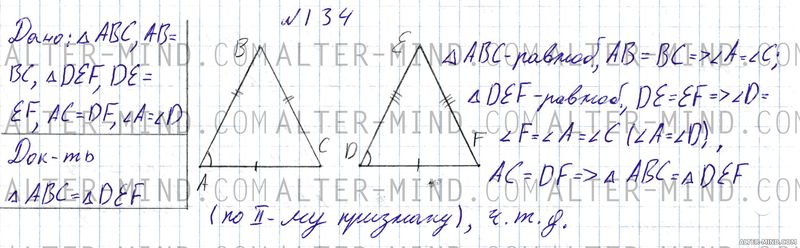
Построим два равных (их равенство докажем ниже) равнобедренных треугольника  ABC и DEF с основаниями AC и DF соответственно. По условию: AB = BC, DE = EF, AC = DF, углы A и D равны. 
В равнобедренном треугольнике углы при основании равны, следовательно углы A и C равны (треугольник ABC - равнобедренный, AC - основание), аналогично равны и углы D и F (треугольник DEF - равнобедренный, DF - основание). Углы A и D равны по условию, следовательно ∠A = ∠C = ∠D = ∠F, DE = EF, следовательно треугольники ABC и DEF равны по второму признаку равенства треугольников, что и требовалось доказать.

Решение:

Открыть картинку в новой вкладке
Другие номера доступны по ссылке