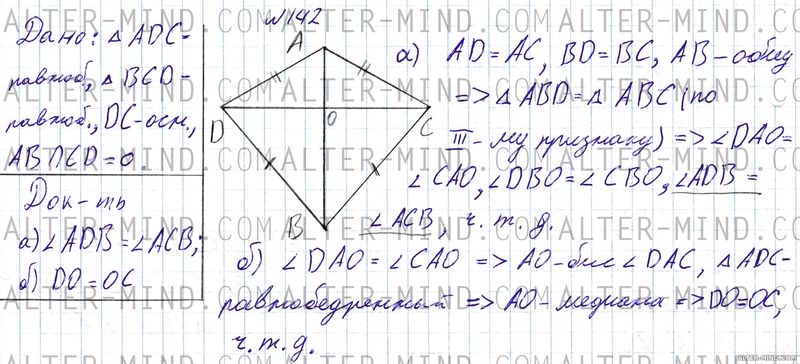
№142 Геометрия 7 класс Атанасян
|
Прочитаем задачу №142 для седьмого класса учебника Атанасян:
Объяснение:
Строим равнобедренные треугольники ADC и BCD c общим основанием DC (вариант чертежа можно посмотреть в решении. Возможен другой вариант построения, где один треугольник будет находится внутри другого, решение, в этом случае, отличаться не будет).
а) AD = AC (боковые стороны равнобедренного треугольника ADC), BD = BC (боковые стороны равнобедренного треугольника BCD), AB - общая сторона, следовательно треугольники ABD и ABC равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠DAO = ∠CAO, ∠DBO = ∠CBO, ∠ADB = ∠ACB, что и требовалось доказать (нужное равенство подчеркнуто). б) ∠DAO = ∠CAO, следовательно AO - биссектриса угла DAC, а поскольку треугольник ADC - равнобедренный AO - медиана, следовательно DO = OC, что и требовалось доказать. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (30.10.2018) | |
| Просмотров: 2756 |
| Всего комментариев: 0 | |