|
Прочитаем задачу №155 для седьмого класса учебника Атанасян:
С помощью циркуля и линейки постройте угол, равный а) 45° б) 22°30'
Каждую букву разберем отдельно. Для удобства и компактности построения будем использовать дуги вместо окружностей.
а) 45°
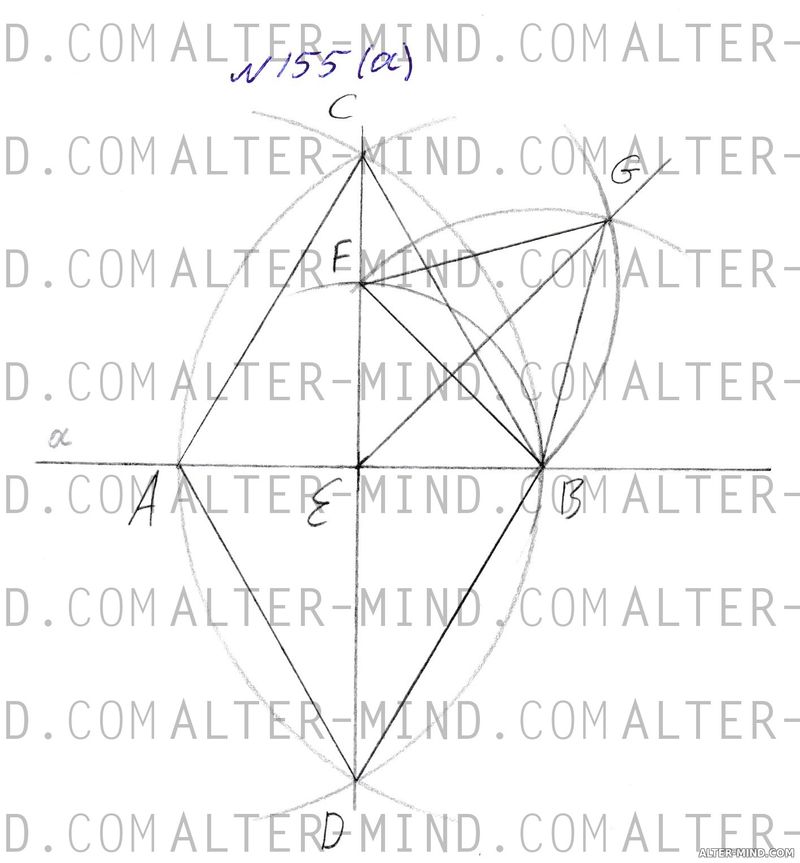
- Проведём прямую a и отметим на ней точку A. На произвольном расстоянии от A отметим точку B.
- Проведём пересекающиеся дуги окружностей радиуса AB с центрами в точках A и B. Точки пересечения дуг обозначим C и D. Проведём CD, пересекающую отрезок AB в точке E. Проведём отрезки AC, AD, BC и BD.
- Проведём дугу радиуса EB с центром в точке E. Точку пересечения этой дуги с отрезком CE обозначим F. Проведём отрезок BF.
- Проведём дуги окружностей радиуса BF с центром в точках B и F. Точку пересечения этих дуг, находящуюся во внутренней области угла BEC обозначим G. Проведём отрезки EG, FG и BG.
- Докажем, что угол BEG - искомый (равен 45°): AC = AD = BC = BD (радиусы AB), СD - общая сторона, следовательно треугольники ACD и BCD равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠ACD = ∠BCD, следовательно биссектриса (отрезок CE вложен в отрезок CD, который является биссектрисой угла ACB по определению), медиана и высота равнобедренного треугольника ABC (AC = BC), следовательно угол CEB равен 90°. EF = BE (равные радиусы EB), FG = BG (равные радиусы BF), EG - общая сторона, следовательно треугольники EFG и EBG равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠FEG = ∠BEG = 1/2 ∠CEB = 45°, что и требовалось доказать
б) 22°30'
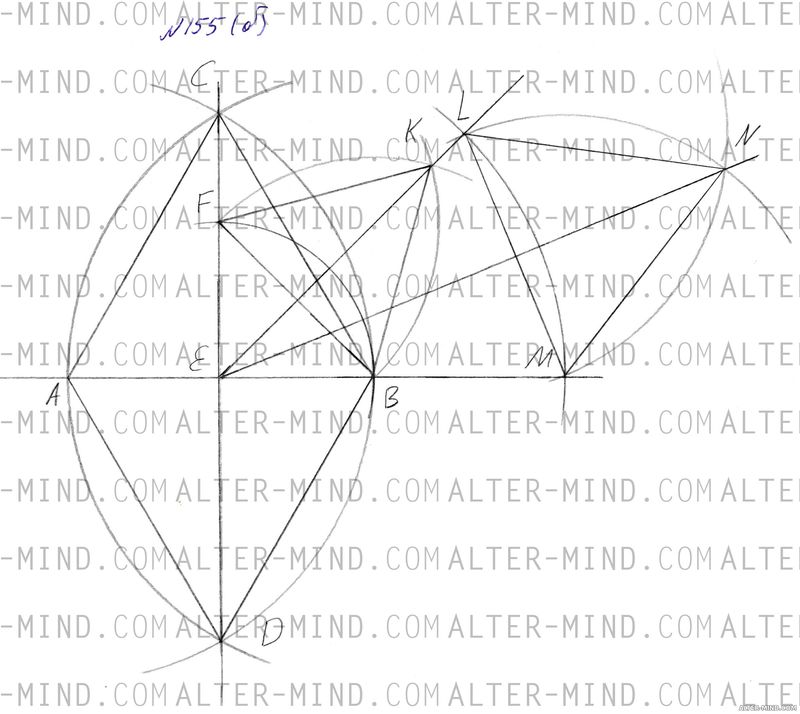
- Проведём прямую AB. Проведём пересекающиеся дуги окружностей радиуса AB с центрами в точках A и B. Точки пересечения дуг обозначим C и D. Проведём отрезки AC, AD, BC, BD и CD. CD пересечет AB в точке E.
- Проведём дугу окружности радиуса EB с центром в точке E. Эта дуга пересечёт отрезок CE в точке F. Проведём отрезок BF.
- Проведём пересекающиеся дуги окружностей радиуса BF c центрами в точках B и F. Точку пересечения дуг во внутренней области угла CEB обозначим K. Проведём отрезки KF и KB.
- Проведём дугу окружности произвольного радиуса r с центром в точке E. Точки пересечения этой дуги с лучами EK и EB обозначим L и M соответственно. Проведём отрезок LM.
- Проведём пересекающиеся дуги окружностей радиуса LM с центрами в точках L и M. Точку пересечения этих дуг во внутренней области угла KEB обозначим N. Проводим отрезки LN, LM и EN.
- Докажем, что угол NEM - искомый (равен 22°30'): AC = AD = CB = BD (радиусы AB), СD - общая сторона, следовательно треугольники CAD и CBD равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠ACD = ∠BCD, следовательно CE - биссектриса (CE является частью отрезка CD, а CD - биссектриса угла ACB по определению), медиана и высота равнобедренного треугольника ABC (AC = BC), следовательно угол CEB равен 90°. EF = BF (радиусы EB), KF = KB (радиусы BF), EK - общая сторона, следовательно треугольники EFK и EBK равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠FEK = ∠BEK = 1/2 ∠FEB (совпадает с углом CEB). EL = EM (радиусы r), LN = MN (радиусы LN), EN - общая сторона, следовательно треугольники ELN и ELM равны по третьему признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠LEN = ∠NEM = 1/2 ∠LEM (совпадает с углом BEK) = 1/4 ∠CEB = 22°30'. Т.е. ∠NEM = 22°30', что и требовалось доказать.
|