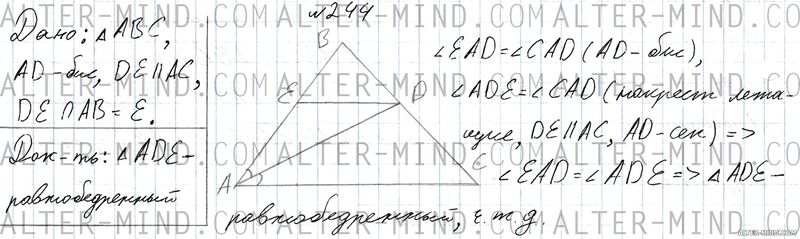
№244 Геометрия 7 класс Атанасян
|
Прочитаем задачу №244 для седьмого класса учебника Атанасян:
Объяснение:
∠EAD = ∠CAD (AD - биссектриса), ∠ADE = ∠CAD (накрест лежащие при параллельных прямых DE и AC, AD - секущая), следовательно углы EAD и ADE равны, следовательно треугольник ADE - равнобедренный (углы при основании равны), что и требовалось доказать.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (19.03.2019) | |
| Просмотров: 1775 |
| Всего комментариев: 0 | |