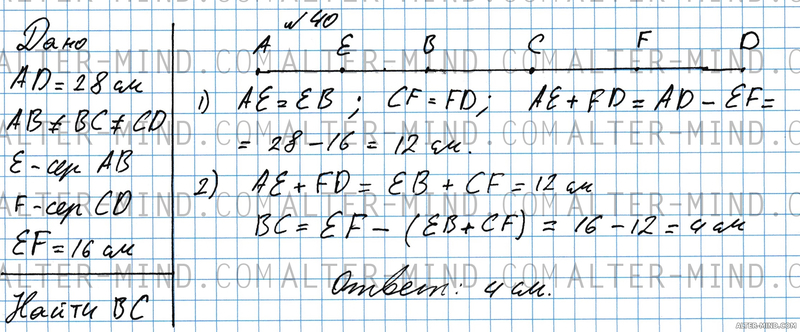№40 Геометрия 7 класс Атанасян
Прочитаем задачу №40 для седьмого класса учебника Атанасян:
Отрезок, равный 28, разделен на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка. Объяснение:
Построим отрезок AB. Из точки B проведем отрезок BC, так чтобы они лежали на одной прямой и не были равны. Аналогично, из точки C проведем отрезок CD. Получаем отрезок AD, разделенный на три неравных отрезка. Отмечаем точку E - середину отрезка AB и точку F - середину отрезка CD.
1) AE = EB и CF = FD т.к. точки E и F середины отрезков AB и CD соответственно. Отрезок EF - это расстояние, между серединами крайних отрезков, по условию равное 16 см. Если из всего отрезка AD "вырезать" отрезок EF, то останутся два отрезка: AE и FD. Находим их суммарную длину, вычитая из большого отрезка известную часть. 2) Суммы отрезков AE + FD и EB + CF равны, т.к. они являются равными половинками отрезков AB (первое слагаемое) и CD (второе слагаемое). Получаем, что отрезок BC = EF - (EB + CF). См. построение в решении. | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (12.09.2018) | |
| Просмотров: 1580 |
| Всего комментариев: 0 | |