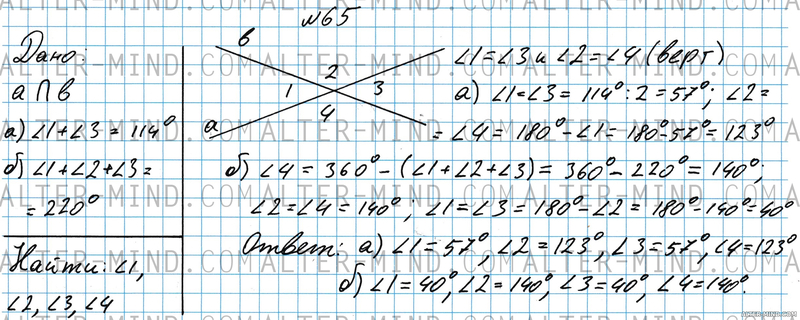№65 Геометрия 7 класс Атанасян
|
Прочитаем задачу №65 для седьмого класса учебника Атанасян:
Объяснение:
При пересечении двух прямых образуется 4 угла. (две пары вертикальных и 4 пары смежных углов). Рассмотрим отдельно случаи а) и б):
а) поскольку сумма смежных углов равна 180°, а у нас сказано что два из четырех углов равны 114° можно утверждать, что сумма двух вертикальных углов в нашем случае равна 114°. (У нас всего 4 угла. Если мы возьмем любые 2 из них они будут либо вертикальными (читай: равными друг другу), либо смежными (читай: их сумма 180°)). Получаем ∠1 = ∠3 = 114°:2 = 57°. Углы 2 и 4 будут вертикальными между собой и смежными по отношению к углам 1 и 3. Находим их: ∠2 = ∠4 = 180° - ∠1 = 123°. б) Сумма всех 4 углов при пересечении двух прямых всегда будет равна 360° (можно представить как сумму двух пар смежных углов или сумму двух развернутых углов). Поскольку нам известна сумма трех углов, можем найти оставшийся угол: ∠4 = 360° - (∠1 + ∠2 + ∠3) = 140°. Остальные углы найти легко. Углы 4 и 2 вертикальные (значит они равны) и смежные по отношению к углам 1 и 3. Находим оставшиеся углы аналогично случаю в букве а). | |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (18.09.2018) | |
| Просмотров: 4935 |
| Всего комментариев: 0 | |