№173 Геометрия 7 класс Атанасян
|
Прочитаем задачу №173 для седьмого класса учебника Атанасян:
Объяснение:
Существует несколько способов решения этой задачи. Первый способ использует только те геометрические сведения, которые прошли. Второй способ самый короткий, подойдёт для тех, кто изучает материал наперед или делает задачу в качестве повторения пройденного материала. I.Способ: Построим треугольник ABC, на продолжении стороны AC отметим точку D. Получаем что углы ACB и BCD смежные. Нам нужно доказать, что другие два угла (A и B) меньше угла BCD.
1) Проведём медиану AM и продолжим её так, что AM = EM. Проведём EC. 2) Углы AMB и CME равны (вертикальные), AM = EM, BM = MC (AM - медиана), следовательно треугольники ABM и CEM равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠ABM (совпадает с углом B треугольника ABC) = ∠ECM. Так как угол BCD состоит из суммы углов ECM и ECD, можем утверждать, что ∠BCD больше ∠B. Часть необходимого доказана. 3) Продолжим сторону BC треугольника, на продолжении отметим точку K. Проведём медиану BN и продолжим её на равную длину так, что BN = FN. Проведём отрезок CF. 4) Углы ANB и CNF равны (вертикальные), BN = FN (см. п.3), AN = CN (BN - медиана), следовательно треугольники ABN и CFN равны по первому признаку равенства треугольников. В равных треугольниках соответствующие элементы равны: ∠BAN (совпадает с углом A треугольника ABC) = (∠FCN). Углы BCD и ACK равны (вертикальные). Угол ACK состоит из суммы углов FCK и FCN. То есть ∠BCD = ∠FCK + ∠FCN, следовательно угол BCD больше угла A (= ∠FCN). Другая часть необходимого доказана. 5) в пунктах 2 и 4 мы доказали что угол BCD больше угла A и угол BCD больше угла B, что и требовалось доказать. Решение:  Открыть картинку в новой вкладке II Способ (используется сумма углов треугольника, которая будет пройдена позже)
Построим треугольник ABC, на продолжении стороны BC отметим точку D. Получаем что углы ACB и BCD смежные. Нам нужно доказать, что другие два угла (A и B) меньше угла BCD.
1) Сумма углов треугольника равна 180°. Откуда получаем ∠A + ∠B + ∠BCA = 180, откуда получаем: ∠A + ∠B = 180° - ∠BCA. 2) ∠BCA + ∠BCD = , то есть ∠BCD = - ∠BCA. Получаем ∠BCA = ∠A + ∠B, следовательно ∠BCA > ∠A и ∠BCA > ∠B, что и требовалось доказать. Решение: 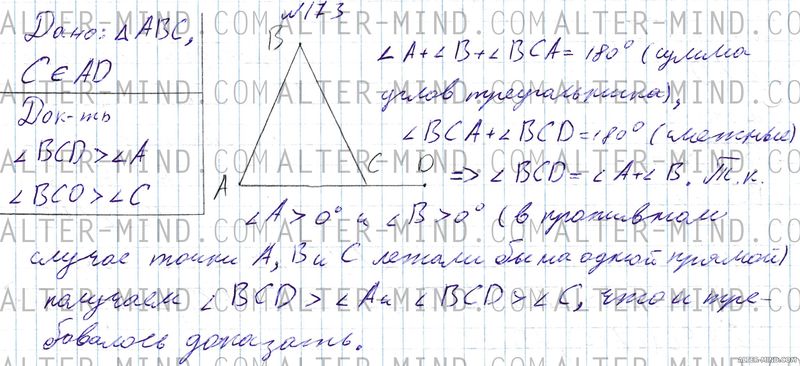 Открыть картинку в новой вкладке Другие номера доступны по ссылке
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (28.11.2018) | |
| Просмотров: 1556 |
| Всего комментариев: 0 | |