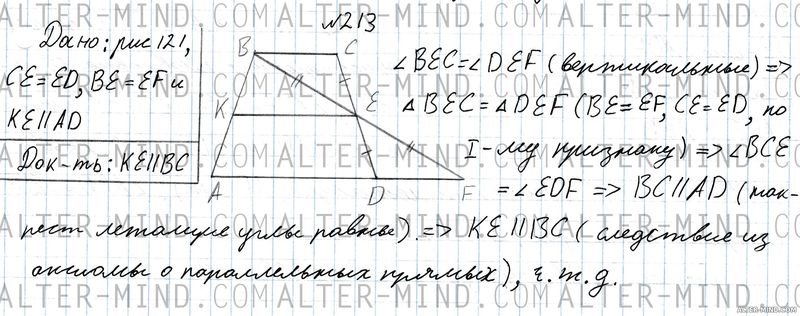
№213 Геометрия 7 класс Атанасян
|
Прочитаем задачу №213 для седьмого класса учебника Атанасян:
Объяснение:
Рассмотрим рисунок 121 учебника (см. чертеж в решении): Углы BEC и DEF равны (вертикальные), следовательно равны и треугольники BEC и DEF (BE = EF, CE = ED по рисунку, значит выполняется первый признак равенства треугольников). В равных треугольниках соответствующие элементы равны: ∠BCE = ∠EDF. Углы BCE и EDF являются накрест лежащими (секущая CD пересекает прямые AD и BC), следовательно прямые KE и BC параллельны (см. признаки параллельности прямых). Так как KE || AD и BC || AD, то KE || BC (если две прямые параллельны третьей прямой, то они параллельны. Следствие из аксиомы о параллельных прямых), что и требовалось доказать.
| |
| Категория: Геометрия 7-9 Атанасян | Добавил: altermind (13.01.2019) | |
| Просмотров: 2198 |
| Всего комментариев: 0 | |