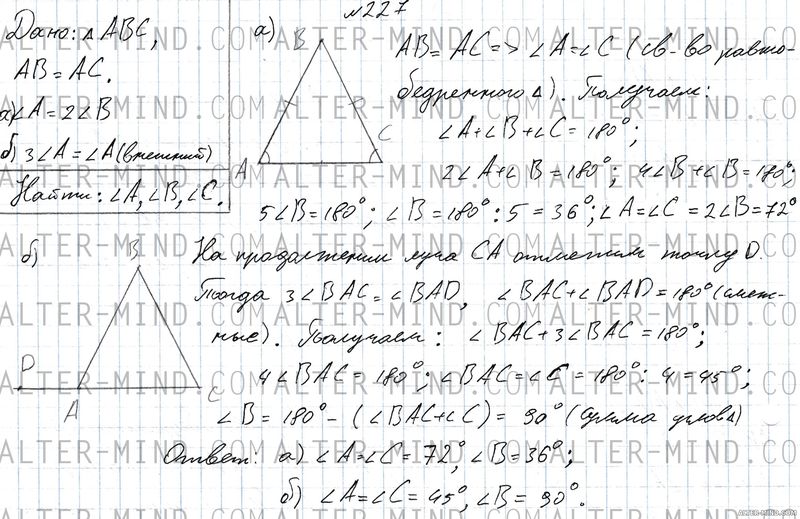Прочитаем задачу №227 для седьмого класса учебника Атанасян:

Объяснение:

---

---

а) В равнобедренном треугольнике ABC углы A и C при основании AC равны. По условию угол A в два раза больше угла B (лежит напротив основания AC). Запишем сумму углов треугольника ABC: ∠A + ∠B + ∠C = 180. Так как ∠A = ∠C и ∠A = 2∠B получаем: 5∠B = 180°, откуда ∠B = 36°, ∠A = ∠C = 72°.
б) На продолжении луча CA (см. чертеж в решении) отметим точку D. Тогда по условию 3∠BAC = ∠BAD. Углы BAC и BAD в сумме составляют 180° (смежные), при этом на угол BAC приходится 3 части, а на угол BAD - одна. Получаем, что угол BAD = 45° (180° / 4) и угол BAC = 135°. Углы BAC и C при основании равнобедренного треугольника равны, через сумму углов треугольника находим угол B.

Решение:

Открыть картинку в новой вкладке
Другие номера доступны по ссылке